Physics and the Human Body

It's interesting to think that our bodies can be described using mechanics and mathematics.However despite how odd it may seem,to compare human physiology to mechanical movements, there surely is an explanation for just about everything with regard to human movement and functionality. Topics include the mechanics of the static body and the body in motion, the materials properties of the body, muscles in the body, the energetics of body metabolism, fluid flow in the cardiovascular and respiratory systems, the acoustics of sound waves in speaking and hearing, vision and the optics of the eye, the electrical properties of the body, and the basic engineering principles of feedback and control in regulating all aspects of function. All such topics aid us in the understanding of how all the things we take for granted in the human body truly work. Biomechanics and Human Movement (Biomechanics being the science concerned with the internal and external forces exerted on the human body and the effects produced from these forces), gives explanation for how simple movements and flexion work through a mathematical understanding.

Two Branches of Biomechanics

Biomechanics is separated into two different categories, or "branches," of study. There is Kinematics, which is the study of human movement from a geometrical standpoint. And there is also Kinetics, the branch of biomechanics concerned with what causes the body to move the way it does. The two branches work had in hand to describe and explain human movements such as Joint Kinematics, Knee Flexion, Ankle Dorsal Flexion, Joint Kinetics, Joint Angles, and the Instantaneous 3D bone pose. There are several Estimable Quantities (referring to simplified equations, using estimated values of its dependent variables), used in discussing the Biomechanics of the Human Body. Such quantities include the Instantaneous 3D bone pose as stared above, which is a virtual representation of the skeletal system in motion, Relative Movement between adjacent bones, dealing with joint kinetics, Forces transmitted by muscles-tendons-ligaments-bones, which also is a aspect of joint kinetics, and Muscular mechanical work/power, which dealing with systems energy, falling under the category of joint energetics. In sum our bodies movements can be described using Kinematics and Kinetics, the prevalent tools in explanation and understanding of how we work.

Joint Kinematics

Anatomical planes and axis are used to describe the human body in Joint Kinematics. The planes include, the Sagittal Plane, a plane parallel to the sagittal suture. The Sagittal plane divides the body into left and right. The transverse plane (also called the horizontal plane, axial plane, or trans axial plane) is an imaginary plane that divides the body into superior and inferior parts. And the Frontal (coronal) plane, which is any vertical plane that divides the body into ventral and dorsal (belly and back) sections.

In the study of Joint Kinematics,body segments are linked to each other at the joints. The joint structure determines the types of joint motions allowed at the joint. Joint motion is actually the relative motion of the distal segment to the proximal that together form a joint. Analytically speaking, it is advantageous to view joint motions as the relative motions between the rigid bodies. Body segments are considered to be ridged bodies, for the purpose of describing the motion of the body, such segments include, the the foot, shank (leg), thigh, pelvis, thorax, hand, forearm, upper-arm and head. Joints between adjacent segments include the ankle (talocrural plus subtalar joints), knee, hip, wrist, elbow and shoulder. Position is used to describe the location of the body segment in conjuncture to the axial planes stated above. A body segment or joint in space is measured in meters, and a related measure called "displacement" refers to the position with respect to starting position. In two dimensions, the position is given in Cartesian coordinates (system is a coordinate system that specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances to the point from two fixed perpendicular directed lines, measured in the same unit of length,) with horizontal variables followed by the vertical position. Heres a quick example of the use of Joint Kinematics and labeling movement. Kinematic measurements are limited in what they can tell us about the causes of motion is - for this we need to look at the kinetics. However, they do provide a description of the motion which can be valuable for certain purposes.

Kinematics of Walking and Running

One important observation we can make from looking at the kinematics of the body is the amount of up-down and sideways motion. In actions such as walking and running, the body is attempting to move horizontally across the ground. However any other motion, especially vertical motion, does not help this objective, and uses upward precious energy.If the body had wheels it could avoid vertical motion altogether, but since we have legs, there must be some vertical motion. The reason for this is that at heel-strike and toe-off the two legs make up the sides of a triangle, while during mid-stance the stance leg is vertical. This has the effect of lowering the upper-body (often called the HAT segment for Head-Arms-Trunk) at heel-strike and toe-off (which together make up the phase known as double stance, when both feet are in contact with the ground), and raising it during mid-stance:

The body's center of mass (CoM), is located in the pelvis. In order for the CoM to rise up between heel-strike and mid-stance, energy must be expanded, the energy is not conserved when it drops at the toe but rather expended. This is an up and down motion of the CoM.

Knee Flexion

When talking about Flexion we are talking about the action of bending or the condition of being bent especially the bending of a limb or joint, in this case the knee. The knee is the largest joint in the body and one of the joints most frequently injured. Most daily activities as well as sports activities require full functional movement of this joint. The knee consists of six articulating surfaces (any surface of a skeletal formation (bone, cartilage) that makes normal direct contact with another skeletal structure as part of a synovial joint,) including, the two condyles (the round prominence at the end of a bone) of the femur, the two condyles of the tibia, the posterior surface of the patella, and a patellar surface on the anterior surface of the femur. The knee joint is essentially a hinge joint capable of flexion and extension, however the knee is not a simple hinge. During flexion and extension the femur moves forwards and backwards respectively over the tibial plateau and during the late stages of extension there is some medial rotation at the joint. (Conversely during the early stages of flexion there is lateral rotation. The joint where the femur and tibia meet must be able to flex, extend and rotate while withstanding large amounts of force exerted on it and relative sliding between components during vigorous activity.

Ankle Dorsal Flexion

Ankles are stability joints that must very quickly absorb force, then help shift and stabilize weight for the next movement. The ankle joint is a synovial hinge (class of "hinge" in the body including ankle, elbow and knee) composed of the talus, fibula, and tibia. The ankle absorbs 85% of the weight pressing down on the foot during standing. This joint allows for dorsiflexion and plantar flexion. Dorsiflexion, is flexion of the foot in an upward direction in the case of the ankle in the positive direction. Where as plantar flexion is the movement of the foot that flexes the foot or toes downward toward the sole, in this case negative.

Joint Kinetics

Kinetics can be defined as being the scientific study of the turnover, or rate of change, of a specific factor in the body, commonly expressed as units of amount per unit time. The Human body is a system of rigid segments inter-linked at the joints. One of the most important aspects of this type of system is the interaction between the inter-linked segments at the joints. The joints (ligaments, joint capsule, etc.) themselves are passive structures that only apply constraining forces, when they are stretched, on to the bony structures involved in the joints. The active components of the system are the skeletal muscles that produces forces through voluntary contraction. Through a process called inverse dynamics one can asses the interaction between the segments through the joint & muscle and the work done by the muscles. Inverse dynamics literally means that one tries to figure out the cause of motion based on the effects (motion) and the inertial properties of the object in motion. One can quantify the human (or animal) motion through motion analysis. The inertial properties of the segments can be obtained from direct or indirect methods. The human body is most accurately described as being the "linked segment system," in which the natural assumption is that the joints are all pin joints and there is no friction at the joint. Thus, the forces produced by the elements of the joint such as ligaments and joint capsules are all concentric about the joint centers. In other words, all these forces pass through the joint centers. That muscles are the only elements that can produce eccentric forces about the joint centers. And that all muscles are uni-articular and there is no intervening structure that can act as pulley. In other words, muscles are straight and directly attach to the segments. Such a procedure will be later describe through the use of Joint Energetics.

Joint Angels

Joint angle (also called inter-segmental angle) is the simply the angle between two segments on either side of the joint, usually measured in degrees and often converted to mathematical notation. Since joint angles are relative to the segment angles, they don't change with the body orientation.

On the other hand segment angles are quite different. Segment angles are angles of the segment with respect to the right-hand horizontal. Segment angles are absolute measurements, that change according to the orientation of the body.

You can apply basic physics knowledge when finding joint angels. The use of velocity in movement has proven to be very useful. Velocity (distance moved / time taken ) is another word for speed. Velocity may be linear (change in position) measured in meters per second (m/s or ms-1), or angular (change in angle), measured in degrees per second (deg./s or deg.s-1). Normally, velocity is derived from position or angle data by the process of differentiation. For example: If a knee moves from a horizontal position of 1.5 m to a position of 1.6 m in 1/50 of a second, it has a velocity of Velocity = (1.6 - 1.5) / (1/50) = 0.1 x 50 = 5 ms-1. Acceleration is also valuable when addressing Joint angles. Acceleration is the change in velocity. Again, it may be linear (change in linear velocity) measured in meters per second per second (m/s2 or ms-2), or angular (change in angular velocity), measured in degrees per second per second (deg./s2 or deg.s-2). Acceleration, too, is usually calculated from the position data by differentiating twice. It can also be measured directly by an instrument called an accelerometer.

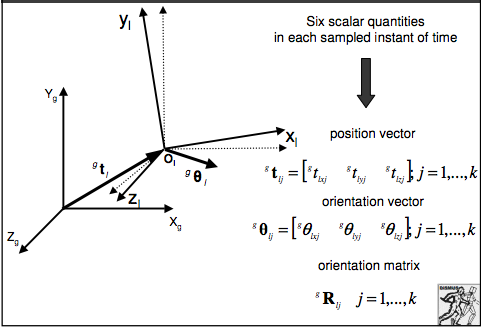
Instantaneous 3D bone pose

In order to describe the pose of the bones in a ridged body we use a reference frame with local coordinates using bone points and invariant time. This reference frame is called the instantaneous 3d bone pose.

The most complicated aspect of the pose is the mathematical description. One must describe the position and orientation of the bone (local reference plane) with respect to a global reference plane.

In the case of the 3D bone pose there are six scaler quantities, each on a sampled instant of time, a position vector, orientation vector, and a orientation matrix. The orientation matrix of the local frame with respect to the global one is defined by a 1st column the xl axis versor (Versor is a templated class that holds a unit quaternion. The difference between versors and quaternions is that quaternions can represent rotations and scale changes while versors are limited to rotations) components, the second column, the yl axis versor components, and the third column, the zl axis versor components. The three components stated above are the cosines of the angles between each versor and the XYZ global axes. Here is a numerical description of the pose vs time (3-D case).

Forces Transmitted by Muscles-Tendons-Ligaments-Bones

Movement occurs through the coordinated working of bones, tendons and ligaments. All three pertinent parts of the human body work together in response to neurological signals, and if there is any disease or condition that interrupts the nerves' signals or if there is any injury to any of these structures, movement can be hindered. In order to gather a fuller understanding lets recount what tendons, bones and ligaments are. Tendons are tough bands of connective tissue found in the joints. They connect muscles to bones. Each muscle has tendons attached at each end. Tendons are designed to only stretch a small amount. Their job is to transmit force between the bones and the muscles. For example, when the biceps muscle on the front top of the arm contracts, the tendon attached to the biceps muscle and elbow bone helps the muscle to pull on the elbow bones so the joint can bend. Ligaments are made of the same material as tendons. Ligaments connect the bones to each other, and are designed to help stabilize the joints and provide a structure for the bones. Since they have limited stretching ability, they limit how far a joint moves to help protect against injury. As the elbow joint bends, the ligaments stabilize the elbow bones so the arm can move with control.

Muscles in the body contract or shorten when they receive nerve signals initiated by the brain. There are three types of muscles including, skeletal muscles, which can be voluntarily controlled, involuntary smooth muscles, such as those that control breathing, digestion and other functions, and involuntary cardiac muscles, which control the function of the heart. Skeletal muscles travel across the length of joints and stretch between the bones.

Forces transmitted by muscles can be illustrated using Internal Load Modeling. Muscles, ligaments and tendons are treated as ropes, thus there is no 3D modeling for their forces. Internal Load Modeling does not take into account any interaction with surrounding muscles and bony structures. For each body segment of interest, the following quantities are estimated: the position vector and orientation matrix relative to both the laboratory frame (g)  and the anatomical frame (a), plus the local position vector of the intersegmental loads which is represented by reduction point K.

The left most diagram below depicts forces acting outward on the knee structure, and to the right shows the forces acting downward on the lower half of the leg.

Kinematic quantities and Inertia parameters are taken into consideration when using Internal Load Modeling as well as the forces shown above. For each body segment of interest, the following quantities are estimated in addition to the ones stated above... Mass is taken into consideration represented by m and K is no longer an arbitrary point.  The local position vector is represented by the notation CM (note in the equation CM is broken up into sub vectors) and the principal axes of inertia by I. The orientation matrix a is also considered as well as moments of inertia. All such things are coupled together to estimate Intersegmental Force (the force between two segments,) as represented in the equation below.

Muscular Mechanical Work/Power & Joint Energetics

Muscle mechanical work is an important biomechanical quantity in human movement. Power is defined as the rate of work or the rate of energy flow. Two power measures can be obtained from the joint kinetics: the joint power and the muscle power. The joint power is the scalar product of the net joint force and the joint velocity (P(j)=F*V)where P(j) = the joint power, F = the net joint force, and v = the velocity of the joint. Precisely speaking, the joint power is the rate of energy transfer through the joint caused by the linear motion of the joint.

where FAK/FT = the net joint force acting on the foot at the ankle, FAK/SH = the net joint force acting on the shank at the ankle, and vAK = the ankle velocity. [3] shows that both the foot and leg joint powers are of the same magnitude with an opposite sign at the ankle. This suggests that the ankle joint only transfers energy from foot to the leg and vice versa. Between the two segments forming a joint, one segment always gains energy at the rate the other loses its energy and vice versa.

Muscle power on the other hand is a scaler product of joint torque and the segment's angular velocity (P(m)=T*w)where P(M) = the muscle power, T = the joint torque, and w = the angular velocity. When looking at muscle powers of the foot and the leg at the ankle we can conclude...

where TAK/FT = the ankle joint torque acting on the foot, TAK/SH = the ankle joint torque acting on the lrg, wFT = the angular velocity of the foot, and wSH = the angular velocity of the leg. It appears that there is no apparent relationship between the muscle powers of the foot and leg since the angular velocities of the foot and leg can be very different.At the muscle, two things happen: (1) the muscle transfers energy from one segment it attaches to to the other, and (2) the muscle does work through contraction. The energy transfer happens from one segment to the other and the net change in the energy in the two segments due to the energy transfer must be 0. On the other hand, an individual muscle can either add (positive work) or drain (negative work) energy to or from both segments at the same time by doing work. The angular momentum is shown in figure 2.

Selective Glossary

energetics the branch of science dealing with the properties of energy and the way in which it is redistributed in physical, chemical, or biological processes. Thoracic Centra Middle segment of the vertebral column, there are 12 Thoracic vertebrae between the cervical and the lumbar vertebrae sagittal suture The dense fibrous central tissue between the two parietal bones of the scul, begin to close at age 29 and is fully closed by the age of 35. distal segment The portion of the joint furthest from the body Proximal segment opposite of distal segment, the segment nearest to the center of the body. Cartesian coordinates system is a coordinate system that specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances to the point from two fixed perpendicular directed lines, measured in the same unit of length, synovial joint A synovial joint, also known as diarthrosis, joins bones with a fibrous joint capsule that is continuous with the periosteum of the joined bones, constitutes the outer boundary of a synovial cavity, and surrounds the bones' articulating surfaces. The synovial (or joint) cavity is filled with synovial fluid. Pin Joints a mechanical joint that will transmit axial load but will not transmit torque

Reflection on the Research

I began my project believing I would be able to fit all my information into one stop motion animation. It was a struggle for me trying to figure out how I would be able to pack all of my research and hard work into one video less than 5 minutes long. However I came to the harsh realization that I just would not be able to do so. I discussed with my teacher Mr. Lyke  about adding a website link to my video where I would display all of my research. I had already decided on researching Biomechanics and the human body, and had a basic layout for what I wanted to discuss in my project. I did basic research and had an understanding about what Kinematics and Kinetics was prior to the construction of my website. Once I began constructing my website I was able to expand upon a majority of my concepts I was addressing in comparison to when I was only doing a video. When conducting my research I did a majority through the search engine google scholar. The most challenging part of my project however did not come in finding enough research and understanding the content but rather technological difficulties. The difficulties first began in trying to construct a stop motion and having glitches in the slide timing. Then came constructing a website. I tried multiple system and could not find any easy to use builders. In the end I decided to use Blogger and set it up as it was a website, with tabs and non sequential order. I added a link to my video on the website and a link to website on my you tube account. All in All I am fairly happy with the work I did and with my website. I throughly enjoyed connecting human movement to physics and found a lot of fascinating websites and informative research.

Works Cited

Works Cited

A., and Advanced Technologies For Neuro-Motor Assessment And Rehabilitati. ADVANCED TECHNOLOGIES FOR NEURO-MOTOR ASSESSMENT AND REHABILITATION BIOMECHANICS OF HUMAN MOVEMENT (n.d.): n. pag. Web.

Bartlett, Roger. "Introduction to Sports Biomechanics." (1997): n. pag. Web.

"Biomechanical Analysis of Fundamental Human Movements - Arthur Chapman." Human-kinetics. N.p., n.d. Web. 10 Dec. 2015.

"Biomechanical Analysis of Fundamental Human Movements - Arthur Chapman." Human-kinetics. N.p., n.d. Web. 10 Dec. 2015.

"MVS 330: Biomechanics of Human Movement." MVS 330: Biomechanics of Human Movement. N.p., n.d. Web. 10 Dec. 2015.